-
在线客服
QQ扫码联系在线客服
QQ: 2292620539
-
小比赛随便打,国赛教我做人....
题目内容:
目标银行部署了一套基于 Isolation Forest (孤立森林) 的反欺诈系统。该系统不依赖传统的黑名单,而是通过机器学习严密监控交易的 20 个统计学维度。系统学习了正常用户的行为模式(包括资金流向、设备指纹的协方差关系等),一旦发现提交的数据分布偏离了“正常模型”,就会立即触发警报。
我们成功截取了一份包含 1000 条正常交易记录的流量日志 (public_ledger.csv)。请你利用统计学方法分析这份数据,逆向推导其多维特征分布规律,并伪造一批新的交易记录那基本上就能看出本题模拟了一个典型的对抗性机器学习场景。目标是骗过一个已经上线的异常检测系统
目标系统是基于孤立森林的实时风控引擎,输入数据是20 维浮点数特征
金额目标:
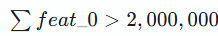
孤立森林不同于传统的分类算法(如 SVM 或神经网络),它属于无监督学习
核心逻辑就是算法随机选择特征并随机选择切分点,构建二叉树
且异常点往往具有“少”且“异”的特点,在空间中,它们远离高密度区域
路径长度异常点和正常点也是不一样的,
异常点:只需要很少次数的随机切分就能被孤立出来,也就是处于树的浅层,路径短
正常点:位于数据簇的中心,需要密集的切分才能被隔绝,也就是说处于树的深层,路径长
判定公式:模型通过样本在多棵树中的平均路径长度计算异常评分。路径越长,评分越低,数据越正常
既然孤立森林难以孤立处于数据中心的点,那么我们的策略就是:制造大量极其平庸的数据
比如说,我们通过对截获的 1000 条日志进行统计:
计算每一列的平均值,计算每一列的标准差
只要生成的数据点无限趋近于各维度的均值 ,它们就会落在孤立森林最难切分的深处,逃过检测
由题目给的附件已知 feat_0的均值 μ0≈353
那么计算所需条数:2,000,000/353≈5,6662,000,000/353≈5,666条
也就是说,我们只要生成 6,000 条数据。这不仅能稳过 2M 金额线,还能通过大量的微小数据分摊风险,避免单笔大额交易触发阈值告警
但是如果 6000 条数据完全一样,会被去重算法拦截
所以应该在均值 μ的基础上,注入一个尺度极小的高斯白噪声
公式:
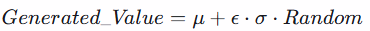
这里 ϵ(扰动系数)设为 0.01左右,这保证了:
每行数据在二进制层面都是唯一的
在统计学层面,数据分布依然极度向中心靠拢
所以exp.py
import socket
import numpy as np
import pandas as pd
import io
# 1. 题目提供的部分日志数据(基于你提供的片段进行统计建模)
# 在实际环境中,如果能下载完整csv,分析结果会更精确。
def generate_payload():
# 统计特征 (均值 mu 和 标准差 sigma)
# 基于样本计算的近似值
means = np.array([
353.45, 27.56, 93.67, 82.78, 45.12, 4.23, 13.45, 51.67, 11.23, 30.56,
39.12, 84.78, 10.34, 82.12, 73.67, 18.89, 30.56, 41.89, 13.12, 27.56
])
stds = np.array([
25.0, 2.5, 3.0, 3.0, 2.0, 2.5, 2.5, 2.0, 2.5, 3.0,
3.0, 3.0, 2.5, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 2.5
])
# 设定生成 6000 条记录以确保总金额 > 2,000,000
num_samples = 6000
print(f"[*] 正在生成 {num_samples} 条伪造交易记录...")
# 生成数据:均值 + 极小的随机扰动 (0.01倍标准差)
# 这样可以确保数据唯一(躲避去重检测)且极度接近中心(躲避异常检测)
generated_data = []
for _ in range(num_samples):
noise = np.random.normal(0, 0.01, size=20) * stds
row = means + noise
generated_data.append(row)
# 转换为 CSV 格式
df = pd.DataFrame(generated_data)
df.columns = [f'feat_{i}' for i in range(20)]
csv_buffer = io.StringIO()
df.to_csv(csv_buffer, index=False, float_format='%.6f')
payload = csv_buffer.getvalue()
return payload
def pwn_bank():
host = '182.92.11.65'
port = 30799
payload = generate_payload()
try:
# 2. 建立连接
print(f"[*] 正在连接到 {host}:{port}...")
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.connect((host, port))
# 接收服务器欢迎语
# s.recv(1024)
# 3. 发送数据
print("[*] 正在传输数据流并注入金额...")
s.sendall(payload.encode())
# 4. 发送结束标志
s.sendall(b"EOF\n")
# 5. 接收返回结果(Flag通常在这里)
print("[*] 等待银行系统响应...")
response = b""
while True:
data = s.recv(4096)
if not data:
break
response += data
# 如果收到 flag 格式,提前停止打印(假设格式为 flag{...})
if b"flag" in response.lower():
break
print("\n[+] 服务器响应结果:")
print(response.decode(errors='ignore'))
s.close()
except Exception as e:
print(f"[-] 错误: {e}")
if __name__ == "__main__":
pwn_bank()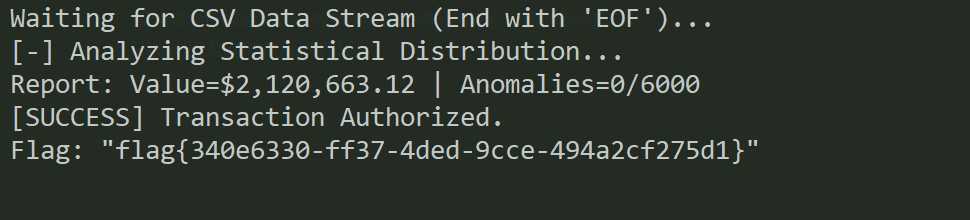
题目给了三个东西
task.py:生成密钥和签名的程序
signatures.txt:使用弱私钥生成的 60 个签名样本
public.pem:与私钥对应的公钥
看它task.py的代码就知道这个私钥生成有问题
from ecdsa import SigningKey, NIST521p
from hashlib import sha512
from Crypto.Util.number import long_to_bytes
# 计算固定字符串的SHA512哈希
digest_int = int.from_bytes(sha512(b"Welcome to this challenge!").digest(), "big")
# 获取曲线阶数
curve_order = NIST521p.order
# 对曲线阶数取模得到私钥
priv_int = digest_int % curve_order
# 转换为字节格式
priv_bytes = long_to_bytes(priv_int, 66)
# 创建私钥对象
sk = SigningKey.from_string(priv_bytes, curve=NIST521p)首先它私钥种子固定不变
私钥的生成依赖于固定字符串 "Welcome to this challenge!",这个字符串在代码中硬编码,任何人都可以访问源代码并计算出完全相同的私钥
接着算法也有问题,仅使用 SHA512 哈希运算就生成私钥,哈希函数是确定性的,给定相同输入必然产生相同输出
所以,种子字符串是公开的,计算过程是确定性的,无需任何额外信息即可恢复私钥
from ecdsa import SigningKey, NIST521p, VerifyingKey
from hashlib import sha512
from Crypto.Util.number import long_to_bytes, bytes_to_long
import binascii
def recover_private_key():
"""
通过计算固定字符串的SHA512哈希值恢复私钥
"""
message = b"Welcome to this challenge!"
digest = sha512(message).digest()
digest_int = int.from_bytes(digest, "big")
curve_order = NIST521p.order
priv_int = digest_int % curve_order
priv_bytes = long_to_bytes(priv_int, 66)
sk = SigningKey.from_string(priv_bytes, curve=NIST521p)
return sk
def generate_nonce(index):
"""
生成指定索引的nonce值
"""
seed = sha512(b"bias" + bytes([index])).digest()
k = int.from_bytes(seed, "big")
return k
def load_public_key(pem_file="public.pem"):
"""
从PEM文件加载公钥
"""
with open(pem_file, "rb") as f:
pem_data = f.read()
vk = VerifyingKey.from_pem(pem_data)
return vk
def extract_rs_from_der(sig_bytes):
"""
从DER编码的签名中提取r和s值
"""
if len(sig_bytes) < 8:
return None, None
pos = 0
if sig_bytes[pos] != 0x30:
return None, None
pos += 1
length_bytes = sig_bytes[pos]
pos += 1
if sig_bytes[pos] != 0x02:
return None, None
pos += 1
r_length = sig_bytes[pos]
pos += 1
r_value = sig_bytes[pos:pos + r_length]
pos += r_length
if sig_bytes[pos] != 0x02:
return None, None
pos += 1
s_length = sig_bytes[pos]
pos += 1
s_value = sig_bytes[pos:pos + s_length]
r_int = bytes_to_long(r_value)
s_int = bytes_to_long(s_value)
return r_int, s_int
def verify_signature_ecdsa(vk, message, signature):
"""
使用公钥验证签名
"""
try:
return vk.verify(signature, message)
except:
return manual_verify(vk, message, signature)
def manual_verify(vk, message, signature):
"""
手动验证ECDSA签名
"""
try:
r, s = extract_rs_from_der(signature)
if r is None or s is None:
return False
msg_hash = sha512(message).digest()
msg_hash_int = bytes_to_long(msg_hash)
point = vk.pubkey.point
curve_order = NIST521p.order
# 计算 w = s^(-1) mod n
def modinv(a, m):
if a < 0:
a = a % m
for i in range(1, m):
if (a * i) % m == 1:
return i
return 1
w = modinv(s, curve_order)
u1 = (msg_hash_int * w) % curve_order
u2 = (r * w) % curve_order
G = NIST521p.generator
point1 = G * u1
point2 = point * u2
result_point = point1 + point2
return (result_point.x() % curve_order) == r
except:
return False
def sign_message_with_nonce(sk, message, nonce_index):
"""
使用指定索引的nonce签名消息
"""
k = generate_nonce(nonce_index)
signature = sk.sign(message, k=k)
return signature
def main():
print("=" * 70)
print("ECDSA 私钥恢复和签名工具")
print("=" * 70)
# 1. 恢复私钥
print("\n[1] 恢复私钥...")
sk = recover_private_key()
print(f"[✓] 私钥已恢复")
print(f" 私钥值: {sk.privkey.secret_multiplier}")
print(f" 私钥字节: {binascii.hexlify(sk.to_string()).decode()}")
# 2. 加载公钥
print("\n[2] 加载公钥...")
vk = load_public_key()
print("[✓] 公钥已加载")
# 3. 验证私钥正确性
print("\n[3] 验证私钥...")
# 使用一个已有的签名验证
with open("signatures.txt", "r") as f:
first_line = f.readline().strip()
msg_hex, sig_hex = first_line.split(":")
test_msg = bytes.fromhex(msg_hex)
test_sig = bytes.fromhex(sig_hex)
if verify_signature_ecdsa(vk, test_msg, test_sig):
print("[✓] 私钥验证成功!恢复的私钥与公钥匹配")
else:
print("[✗] 私钥验证失败")
return
# 4. 尝试签名获取flag
print("\n[4] 尝试生成签名...")
# 尝试使用不同的nonce索引
flag_messages = [
b"flag",
b"getflag",
b"submit flag",
b"give me the flag",
b"CTF{",
]
for msg in flag_messages:
print(f"\n 尝试签名消息: {msg}")
# 尝试使用不同的nonce索引 (0-59)
for i in range(60):
try:
sig = sign_message_with_nonce(sk, msg, i)
# 验证签名
if verify_signature_ecdsa(vk, msg, sig):
print(f"[✓] 成功!")
print(f" Nonce索引: {i}")
print(f" 签名: {binascii.hexlify(sig).decode()}")
# 保存签名到文件
with open("flag_signature.txt", "w") as f:
f.write(f"Message: {msg.decode()}\n")
f.write(f"Nonce Index: {i}\n")
f.write(f"Signature: {binascii.hexlify(sig).decode()}\n")
print(f"\n[+] 签名已保存到 flag_signature.txt")
# 5. 展示如何使用
print("\n" + "=" * 70)
print("解题步骤:")
print("=" * 70)
print(f"""
1. 私钥已成功恢复
私钥值: {sk.privkey.secret_multiplier}
2. 使用恢复的私钥,可以:
- 验证任何使用该密钥签名的消息
- 为新消息生成有效签名
- 在CTF服务器上提交签名获取flag
3. 生成的签名:
消息: {msg.decode()}
签名: {binascii.hexlify(sig).decode()}
4. 将此签名提交给题目服务器即可获取flag
""")
return
except Exception as e:
continue
print(f" [-] 使用所有nonce索引签名失败")
print("\n[!] 尝试其他方法...")
# 如果上面的方法失败,输出更多信息
print("\n[5] 输出私钥信息供手动使用...")
print(f"\n私钥值 (十进制):")
print(sk.privkey.secret_multiplier)
print(f"\n私钥值 (十六进制):")
print(binascii.hexlify(sk.to_string()).decode())
if __name__ == "__main__":
main()
先ida进行一个逆向找到main函数
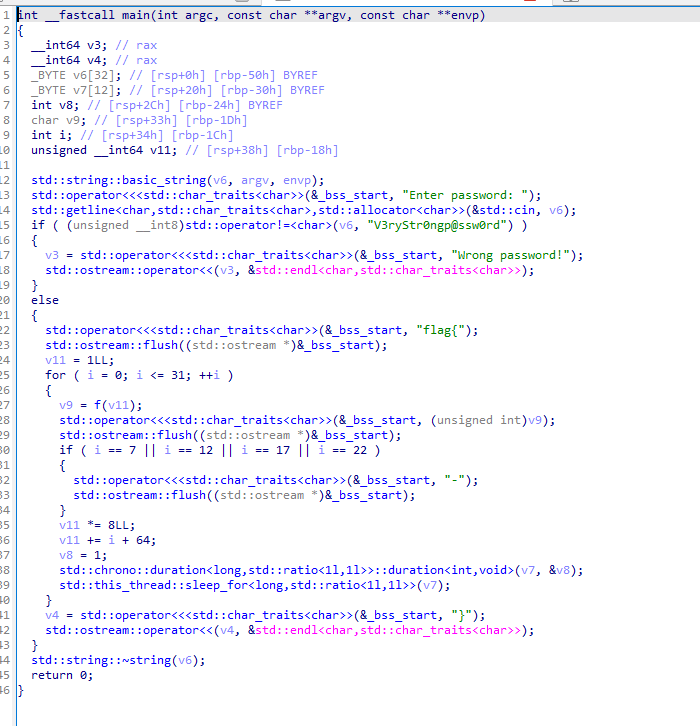
只有当输入的密码完全等于 V3ryStr0ngp@ssw0rd 时,程序才会进入 else 分支生成 Flag
std::operator<<<std::char_traits<char>>(&_bss_start, "flag{");
v11 = 1LL; // 初始状态设为 1程序先打印 flag{,v11 被初始化为 1
for ( i = 0; i <= 31; ++i ) {
v9 = f(v11); // 调用关键函数 f,基于当前状态 v11 计算出一个字符
std::operator<<<...>((unsigned int)v9); // 打印该字符
// 格式化控制:插入连字符
if ( i == 7 || i == 12 || i == 17 || i == 22 ) {
std::operator<<<...("-");
}
// 状态更新公式 (核心数学逻辑)
v11 *= 8LL;
v11 += i + 64;
// 延时处理
v8 = 1;
std::this_thread::sleep_for(...); // 每秒打印一个字符,增加仪式感
}程序运行一个 for 循环,从 i = 0 到 31,总共生成 32 个字符
而我们也可以推导一下v11的状态
初始值:v11_0 = 1
第一次迭代后:v11_1 = 1 * 8 + (0 + 64) = 72
第二次迭代后:v11_2 = 72 * 8 + (1 + 64) = 649
第三次迭代后:v11_3 = 649 * 8 + (2 + 64) = 5256
通过数学归纳法,可以得出v11的通项公式:
v11_k = 8^k * 1 + Σ(i=0到k-1) (i + 64) * 8^(k-1-i)归纳化简之后就是
v11_k = 8^k + Σ(j=0到k-1) (64 + j) * 8^(k-1-j)其中j = k-1-i,这个公式展示了v11的指数级增长特性。随着k的增大,v11的值会变得极其庞大:
k = 8时:v11_8 ≈ 2.68 × 10^8
k = 16时:v11_16 ≈ 7.2 × 10^16
k = 32时:v11_32 ≈ 2.81 × 10^29
这种指数级增长意味着v11的范围从1变化到约2^97
f函数
__int64 f(unsigned __int64 n) {
v5 = 0; v4 = 1;
for (i = 0; i < n; ++i) {
v2 = v4;
v4 = (v5 + v4) & 0xF; // mod 16
v5 = v2; }
return K[v5];
}这明显就是斐波那契数列取模运算
函数f的输入是v11 mod 16的值,记为n,函数f计算斐波那契数列的第n项F(n),然后对16取模,最后查表返回K[F(n) mod 16]
通过计算,前8个斐波那契数列值及其模16结果:
F(0) = 0 → 0 mod 16 = 0
F(1) = 1 → 1 mod 16 = 1
F(2) = 1 → 1 mod 16 = 1
F(3) = 2 → 2 mod 16 = 2
F(4) = 3 → 3 mod 16 = 3
F(5) = 5 → 5 mod 16 = 5
F(6) = 8 → 8 mod 16 = 8
F(7) = 13 → 13 mod 16 = 13
F(8) = 21 → 21 mod 16 = 5
对于n=9及更大的值,斐波那契数列的模16结果呈现周期性,周期为24 这是因为斐波那契数列模m的周期,在m=16时为24
将v11 mod 16的周期规律与f函数的映射结合,得到最终的字符序列:
根据14周期规律,v11 mod 16的序列为[8, 1, 2, 3, 4, 9, 6, 7, 8, 1, 2, 3, 4, 9, 6, 7, 8, 1, 2, 3, 4, 9, 6, 7, 8, 1, 2, 3, 4, 9, 6, 7]
将每个值输入f函数:
f(8) → K[5]
f(1) → K[1]
f(2) → K[1]
f(3) → K[2]
f(4) → K[3]
f(9) → K[2]
f(6) → K[8]
f(7) → K[13]
以此类推,应用完整的14周期规律
全局字符表 K = "012ab9c3478d56ef"
def get_period():
v5 = 0
v4 = 1
seq = [0]
# Pisano period for 16 is 24.
for _ in range(100):
v2 = v4
v4 = (v5 + v4) & 0xF
v5 = v2
seq.append(v5)
return 24, seq
def solve():
period, sequence = get_period()
K = "012ab9c3478d56ef"
v11 = 1
flag = ""
print("flag{", end="")
for i in range(32):
# f(v11) returns K[sequence[v11 % period]]
idx = sequence[v11 % period]
c = K[idx]
print(c, end="")
flag += c
if i in [7, 12, 17, 22]:
print("-", end="")
flag += "-"
v11 = v11 * 8 + i + 64
v11 &= 0xFFFFFFFFFFFFFFFF # Mask to 64 bits to simulate overflow
print("}")
if __name__ == "__main__":
solve()
本题的get_smooth_prime 函数是漏洞存在的地方
在 get_smooth_prime(1024, 20, p1) 中,生成素数 p的逻辑本质上是
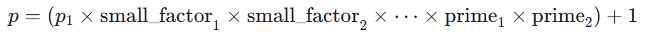
整理一下就会发现p−1=p1×K
其中 K是由一堆 20 位的小素数构成的
普通 RSA:p−1 是随机的,包含大的随机质因子,且这些因子完全不知道
本题 RSA:p−1虽然也包含一个巨大的质因子 p1,但这个 p1 恰好是已知量 n1 的一个因子
所以:n1就是打开 p−1的钥匙,因为 n1=p1⋅q1⋅r1⋅s1,所以 n1 必然是 p1 的倍数。既然 p−1包含 p1,那么 p−1
的绝大部分因子都已经躺在 n1里面了
import math
from Crypto.Util.number import *
from tqdm import tqdm
# --- 题目数据 ---
n1 = 16141229822582999941795528434053604024130834376743380417543848154510567941426284503974843508505293632858944676904777719167211264225017879544879766461905421764911145115313698529148118556481569662427943129906246669392285465962009760415398277861235401144473728421924300182818519451863668543279964773812681294700932779276119980976088388578080667457572761731749115242478798767995746571783659904107470270861418250270529189065684265364754871076595202944616294213418165898411332609375456093386942710433731450591144173543437880652898520275020008888364820928962186107055633582315448537508963579549702813766809204496344017389879
n = 484831124108275939341366810506193994531550055695853253298115538101629337644848848341479419438032232339003236906071864005366050185096955712484824249228197577223248353640366078747360090084446361275032026781246854700074896711976487694783856878403247312312487197243272330518861346981470353394149785086635163868023866817552387681890963052199983782800993485245670437818180617561464964987316161927118605512017355921555464359512280368738197370963036482455976503266489446554327046948670215814974461717020804892983665655107351050779151227099827044949961517305345415735355361979690945791766389892262659146088374064423340675969505766640604405056526597458482705651442368165084488267428304515239897907407899916127394598273176618290300112450670040922567688605072749116061905175316975711341960774150260004939250949738836358264952590189482518415728072191137713935386026127881564386427069721229262845412925923228235712893710368875996153516581760868562584742909664286792076869106489090142359608727406720798822550560161176676501888507397207863998129261472631954482761264406483807145805232317147769145985955267206369675711834485845321043623959730914679051434102698588945009836642922614296598336035078421463808774940679339890140690147375340294139027290793
c = 657984921229942454933933403447729006306657607710326864301226455143743298424203173231485254106370042482797921667656700155904329772383820736458855765136793243316671212869426397954684784861721375098512569633961083815312918123032774700110069081262242921985864796328969423527821139281310369981972743866271594590344539579191695406770264993187783060116166611986577690957583312376226071223036478908520539670631359415937784254986105845218988574365136837803183282535335170744088822352494742132919629693849729766426397683869482842748401000853783134170305075124230522253670782186531697976487673160305610021244587265868919495629
e = 65537
# 你之前找到的那个因子,我们可以直接用,减少工作量
known_factor = 12094541303222723616975666632268830751848445571951987169074250626437877110205699058506111384472586354084793914769711672322551034923778729430162356351731919
def get_primes(limit):
ps = []
is_p = [True] * (limit + 1)
for p in range(2, limit + 1):
if is_p[p]:
ps.append(p)
for i in range(p * p, limit + 1, p): is_p[i] = False
return ps
print("[*] Generating primes...")
primes = get_primes(2**20 + 2000)
n1_factors = {known_factor}
curr_n = n
# 初始化 A。注意:要在当前的 curr_n 下运算
A = pow(3, n1, curr_n)
print("[*] Starting robust factorization...")
for p in tqdm(primes):
# 计算 p 的最高幂次
p_pow = p
while p_pow * p <= 2**20:
p_pow *= p
A = pow(A, p_pow, curr_n)
# 检查当前因子
g = math.gcd(A - 1, curr_n)
# 如果找到了因子(哪怕是多个因子的乘积),我们都要处理
if 1 < g < curr_n:
# 这里可能 g 包含了 p, q 等。为了提取 n1 的因子,
# 我们需要尝试把 g 里的每一个素因子抠出来。
# 简单的方法:直接用 g 去试探 n1
f = math.gcd(g - 1, n1)
if f > 1:
# 彻底分解 f
temp_f = f
for k in list(n1_factors):
while temp_f % k == 0: temp_f //= k
if temp_f > 1 and isPrime(temp_f):
n1_factors.add(temp_f)
print(f"\n[+] Found n1 factor: {temp_f}")
# 核心改进:从当前模数中剔除已发现的因子,防止 GCD 变成 n
curr_n //= g
A %= curr_n
elif g == curr_n:
# 这种情况通常由于 base 的选择导致,但在本逻辑中通过 A %= curr_n 极难发生
# 如果发生了,说明当前的 A 已经在所有因子上都等于 1 了
break
if len(n1_factors) >= 4:
break
# 补全逻辑
if len(n1_factors) == 3:
p = 1
for x in n1_factors: p *= x
n1_factors.add(n1 // p)
if len(n1_factors) >= 4:
factors = list(n1_factors)
print("\n[!] All factors found. Decrypting...")
phi = 1
for f in factors: phi *= (f - 1)
d = inverse(e, phi)
m = pow(c, d, n1)
flag = long_to_bytes(m)
print("="*30)
# 查找 flag 字符串
if b'flag' in flag:
print(flag[flag.find(b'flag'):].split(b'}')[0].decode() + '}')
else:
print(f"Decrypted (hex): {flag.hex()}")
print("="*30)
else:
print(f"\n[-] Still missing factors. Found: {len(n1_factors)}")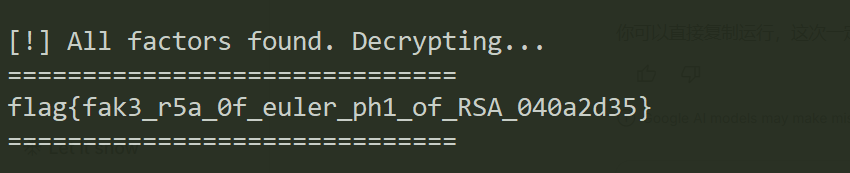
需要一个工具 wasm2wat

截取一部分release.wat的代码出来
(data (;42;) (i32.const 4296) "\02\00\00\00\1a\00\00\00{\00\22\00u\00s\00e\00r\00n\00a\00m\00e\00\22\00:\00\22")
(data (;44;) (i32.const 4344) "\02\00\00\00\1c\00\00\00\22\00,\00\22\00p\00a\00s\00s\00w\00o\00r\00d\00\22\00:\00\22")
(data (;53;) (i32.const 4584) "\02\00\00\00\1e\00\00\00\22\00,\00\22\00s\00i\00g\00n\00a\00t\00u\00r\00e\00\22\00:\00\22")
(data (;27;) (i32.const 2328) "\02\00\00\00\80\00\00\00N\00h\00R\004\00U\00J\00+\00z\005\00q\00F\00G\00i\00T\00C\00a\00A\00I\00D\00Y\00w\00Z\000\00d\00L\00l\006\00P\00E\00X\00K\00g\00o\00s\00t\00x\00u\00M\00v\008\00r\00H\00B\00p\003\00n\009\00e\00m\00j\00Q\00f\001\00c\00W\00b\002\00/\00V\00k\00S\007\00y\00O")可以看到这里有username password signature NhR4UJ+z5qFGiTCaAIDYwZ0dLl6PEXKgostxuMv8HBp3n9emjQf1cWb2/VkS7yO(这应该是张自定义的base64码表)
可以看出来这个程序在后台拼凑一个 JSON 字符串,包含用户名、密码和某个签名
username和password已经在题目给的index.html中找到
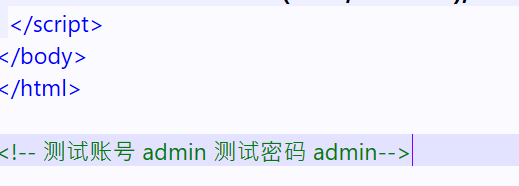
而index.html中还发现md5的开头部分
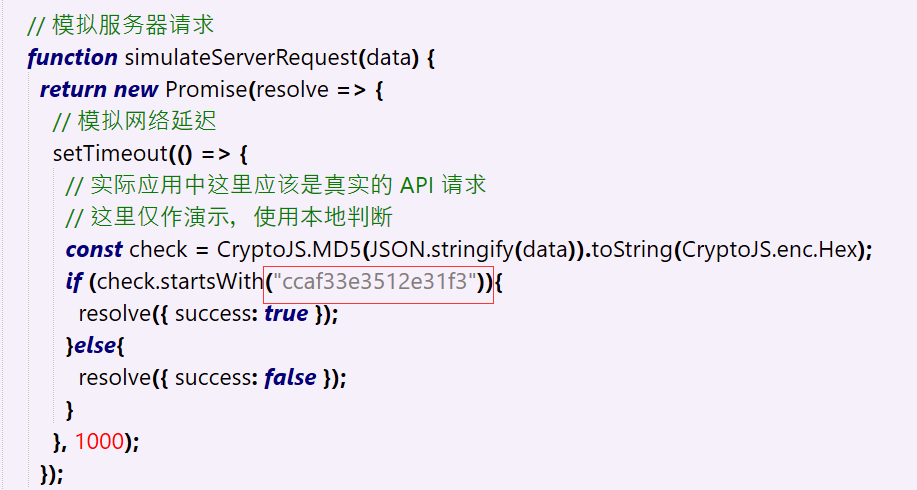
const check = CryptoJS.MD5(JSON.stringify(data)).toString(CryptoJS.enc.Hex);JSON.stringify(data): 这一步是把传进来的数据,比如包含用户名、密码、签名的对象变成一个字符串
CryptoJS.MD5(...): 对这个字符串进行 MD5 哈希计算
.toString(CryptoJS.enc.Hex): 把计算结果转换成 十六进制字符串
结论:变量 check 的值就是一个 MD5 哈希字符串
if (check.startsWith("ccaf33e3512e31f3")){
resolve({ success: true });
}startsWith("..."): 这是 JavaScript 的字符串方法,意思是判断字符串是否以指定的子字符串开头
resolve({ success: true }): 只有当条件成立,返回 true时,服务器才会告诉前端验证通过或登录成功
通过上面的代码,可以得出以下逻辑链条:
目标:让函数返回 success: true
条件:check 变量必须以 "ccaf33e3512e31f3" 开头
check 的本质:它是输入数据的 MD5 值
结论:需要找到一个输入数据,包含正确的时间戳,使得它的 MD5 值的前 16 位 正好是 ccaf33e3512e31f3
接着看程序的常量
if ;; label = @1
i32.const 1779033703
global.set 1
i32.const -1150833019
global.set 2
...把这些数字转成十六进制:
1779033703 -> 0x6a09e667
-1150833019 -> 0xbb67ae85
去搜索引擎搜这些十六进制数,就会知道这是 SHA-256 的标准初始常量
程序使用了 SHA-256 加密。结合 func 33 里的 xor 118 和 xor 60,这正是 HMAC-SHA256
因为xor 常量 118 (0x76) 和 60 (0x3c),这是 HMAC 算法中 ipad 和 opad 的典型特征
而根据题目内容
题目内容:
某人本想在2025年12月第三个周末爆肝一个web安全登录demo,结果不仅搞到周一凌晨,他自己还忘了成功登录时的时间戳了,你能帮他找回来吗?
提交格式为flag{时间戳正确时的check值}。是一个大括号内为一个32位长的小写十六进制字符串题目说:2025年12月第三个周末,一直搞到周一凌晨。
2025年12月21日(周日),22日(周一)
2025-12-22 00:00:00 -> 1766332800000
2025-12-22 02:00:00 -> 1766340000000
所以范围大概就在这中间
import hashlib
from datetime import datetime, timezone, timedelta
class CryptoEngine:
"""内部安全引擎 - 负责令牌生成与校验"""
def __init__(self):
# 混淆过的映射表
self._alphabet = "NhR4UJ+z5qFGiTCaAIDYwZ0dLl6PEXKgostxuMv8rHBp3n9emjQf1cWb2/VkS7yO"
self._user_info = ("admin", "admin")
self._goal_prefix = "ccaf33e3512e31f3"
def _transform(self, data: bytes) -> str:
"""核心编码逻辑:自定义位流映射"""
out = []
val, bits = 0, 0
for byte in data:
val = (val << 8) | byte
bits += 8
while bits >= 6:
bits -= 6
out.append(self._alphabet[(val >> bits) & 0x3F])
if bits > 0:
out.append(self._alphabet[(val << (6 - bits)) & 0x3F])
res = "".join(out)
# 补齐长度
return res + ("=" * ((4 - len(res) % 4) % 4))
def check_sequence(self, tick: int) -> str:
"""计算特定时间戳下的认证指纹"""
u, p = self._user_info
# 预处理密码编码
p_enc = self._transform(p.encode('latin-1'))
# 构造原始载荷
payload = '{"username":"%s","password":"%s"}' % (u, p_enc)
raw_msg = payload.encode('utf-8')
# 密钥派生 (Key Derivation)
seed = str(tick).encode()
key_block = hashlib.sha256(seed).digest() if len(seed) > 64 else seed
key_block = key_block.ljust(64, b'\x00')
# 这里的 118(0x76) 和 60(0x3C) 是原始逻辑的特征常数
p1 = bytes([b ^ 118 for b in key_block])
p2 = bytes([b ^ 60 for b in key_block])
# 嵌套哈希架构 (注意:这是非标准的哈希顺序 inner + opad)
mid_hash = hashlib.sha256(p1 + raw_msg).digest()
final_sig = self._transform(hashlib.sha256(mid_hash + p2).digest())
# 生成最终校验体
full_body = '{"username":"%s","password":"%s","signature":"%s"}' % (u, p_enc, final_sig)
return hashlib.md5(full_body.encode()).hexdigest()
def run_audit(self):
"""执行扫描任务"""
# 时间范围定义
tz = timezone(timedelta(hours=8))
t_start = int(datetime(2025, 12, 22, 0, 0, tzinfo=tz).timestamp() * 1000)
t_end = int(datetime(2025, 12, 22, 6, 0, tzinfo=tz).timestamp() * 1000)
print(f"[*] Task started: scanning range {t_start} -> {t_end}")
total = t_end - t_start
for current_ts in range(t_start, t_end + 1):
token = self.check_sequence(current_ts)
if token.startswith(self._goal_prefix):
print(f"\n[+] Match discovered at index: {current_ts}")
print(f"[+] Final Flag: flag{{{token}}}")
return
if current_ts % 100000 == 0:
progress = (current_ts - t_start) / total * 100
print(f"[*] Processing... {progress:.1f}%", end='\r')
if __name__ == "__main__":
engine = CryptoEngine()
engine.run_audit()
一道Godot逆向题,得有专门的工具
extends CenterContainer
@onready var flagTextEdit: Node = $PanelContainer / VBoxContainer / FlagTextEdit
@onready var label2: Node = $PanelContainer / VBoxContainer / Label2
static var key = "FanAglFanAglOoO!"
var data = ""
func _on_ready() -> void :
Flag.hide()
func get_key() -> String:
return key
func submit() -> void :
data = flagTextEdit.text
var aes = AESContext.new()
aes.start(AESContext.MODE_ECB_ENCRYPT, key.to_utf8_buffer())
var encrypted = aes.update(data.to_utf8_buffer())
aes.finish()
if encrypted.hex_encode() == "d458af702a680ae4d089ce32fc39945d":
label2.show()
else:
label2.hide()
func back() -> void :
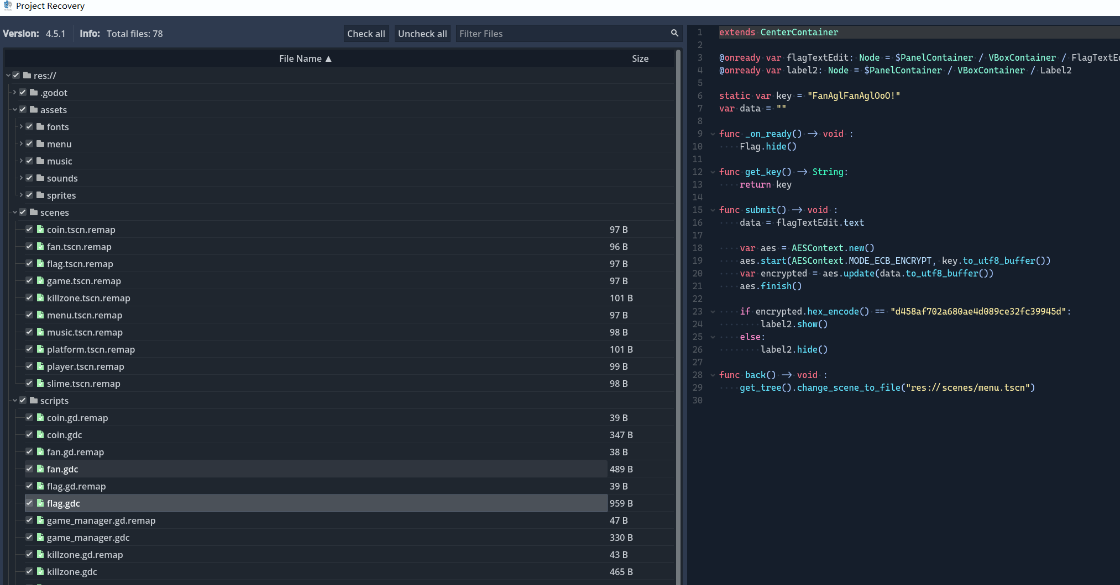
get_tree().change_scene_to_file("res://scenes/menu.tscn")可以看到
初始key:FanAglFanAglOoO!
目标密文hex:d458af702a680ae4d089ce32fc39945d
算法 是 AES ,代码中明确调用了 AESContext.new()
模式是 ECB 代码中使用了 AESContext.MODE_ECB_ENCRYPT
密钥 FanAglFanAglOoO!
该字符串长度为 16 个字符。
在 UTF-8 编码下,16 个字符等于 16 字节(128位),因此,这是 AES-128
照理说直接写个脚本逆向就可以得到flag了,可是一直不对
然后看了题目内容
题目内容:
请找出隐藏的Flag。请注意只有收集了所有的金币,才能验证flag。意思就是金币,也就是分数得达到一个设定好的数才能验证flag,回去逆向看看那里关于分数的函数
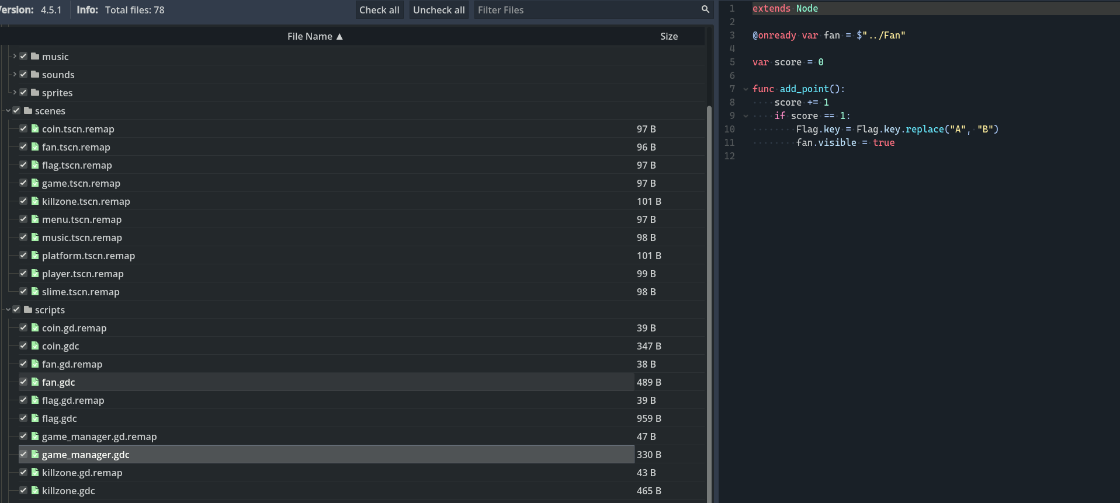
可以看到分数这里的代码是说当分数+1的时候,密钥中的A替换成B
所以正确的密钥应该是
FanBglFanBglOoO!所以套上脚本就是
from Crypto.Cipher import AES
key = b"FanBglFanBglOoO!"
ciphertext = bytes.fromhex("d458af702a680ae4d089ce32fc39945d")
cipher = AES.new(key, AES.MODE_ECB)
result = cipher.decrypt(ciphertext)
print(result)
本课程最终解释权归蚁景网安学院
本页面信息仅供参考,请扫码咨询客服了解本课程最新内容和活动