-
在线客服
QQ扫码联系在线客服
QQ: 2292620539
-
本文是本系列的第三篇,由于侧重点是对密码学中的安全性问题进行分析,所以不会对密码学基础的核心概念进行阐述,如果阅读本系列文章时不明白所涉及的术语时请参考国内大学的推荐教材,如《密码学原理与实践》《深入浅出密码学》,如果只是感兴趣而并非要深入了解,只阅读《图解密码技术》也就够了。
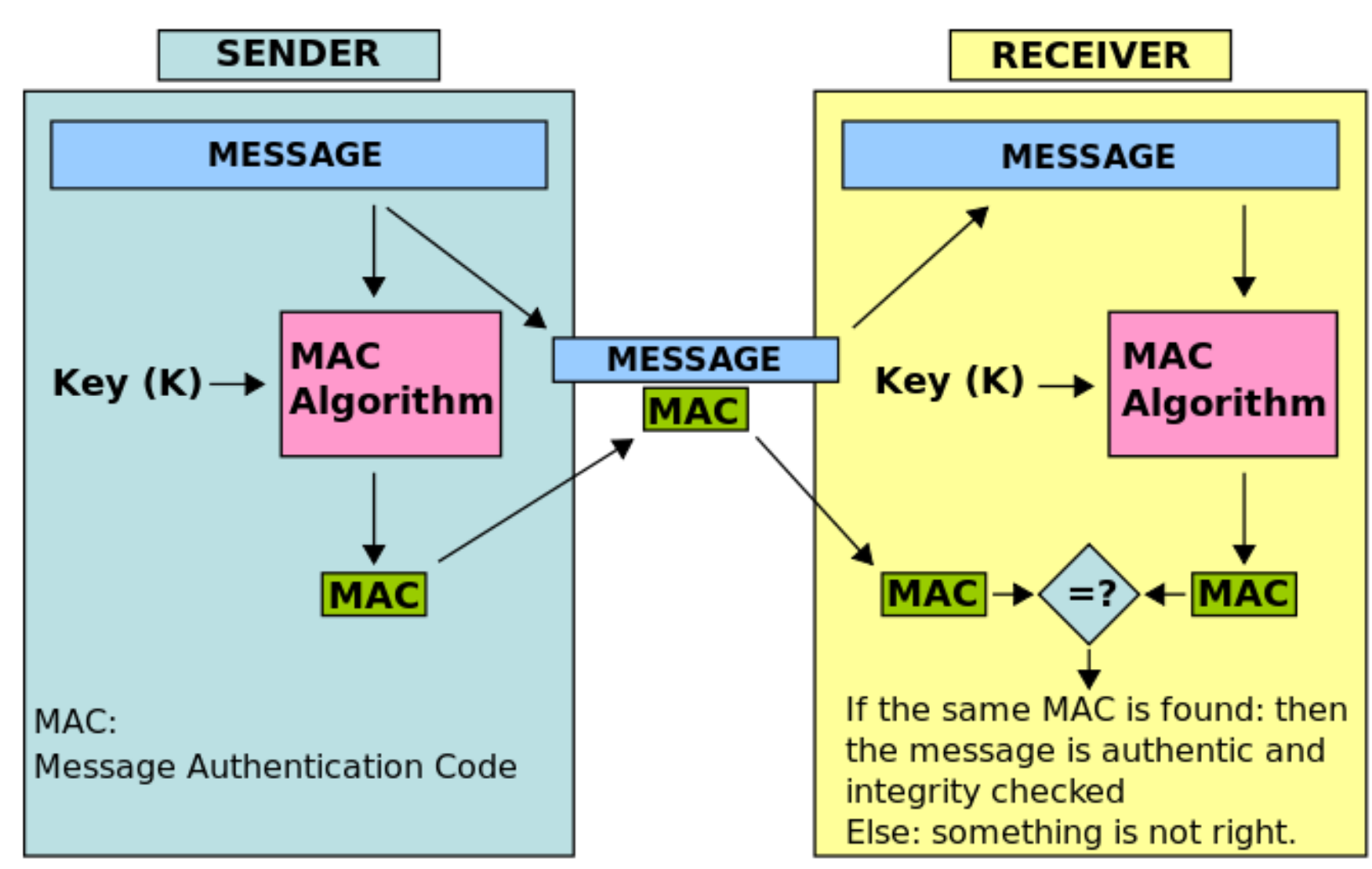
MAC是指消息认证码(带密钥的Hash函数),是密码学中通信实体双方使用的一种验证机制,保证消息数据完整性的一种工具。构造方法由M.Bellare提出,安全性依赖于Hash函数,故也称带密钥的Hash函数。消息认证码是基于密钥和消息摘要所获得的一个值,可用于数据源发送方认证和完整性校验。MAC一般不会从头设计,而是从已有的哈希函数改造而来,比如加前缀、后缀或其他方法。
加前缀时,返回的是Hash(K||M),从而将普通的哈希函数转为带密钥的哈希函数,其容易受到长度扩展攻击、碰撞攻击。
长度扩展攻击我们之前已经提过,在这种攻击场景下,攻击者可以在不知道M1和K的基础上,仅通过Hash(K||M1)就可以计算出Hash(K||M1||M2),相当于攻击者可以伪造有效的MAC标签。
此处的碰撞攻击是由于密钥长度不同导致的。如果密钥K1是24比特的16进制字符串abcdef,消息M1是12,则返回的是Hash(abcded12),如果密钥K2是abcd,消息M2是ef12,则返回的也是Hash(abcded12),这就发生了碰撞
加后缀的方法返回的是Hash(M||K),此时可以抵御长度扩展攻击,但是还是会存在碰撞的问题。
设有两个消息M1,M2,存在碰撞Hash(M1)=Hash(M2),比如在SHA-256中,此时就会存在Hash(M1||K)=Hash(M2||K)
换言之,攻击者通过如下流程即可发动攻击:
1.找到两个碰撞的消息M1,M2
2.请求受害者计算M1哈希的MAC标签Hash(M1||K)
3.猜测相同的Hash(M2||K),从而伪造一个有效的标签并破坏MAC的安全性
HMAC,即散列消息认证码(Hash-based message authentication code),是一种通过特别计算方式之后产生的消息认证码(MAC),使用密码散列函数,同时结合一个加密密钥。它可以用来保证资料的完整性,同时可以用来作某个消息的身份验证。
HMAC从哈希函数构造MAC,这比前面两种方案都安全,IPSec,SSH,TLS等都使用了HMAC
CMAC,Cipher-based Message Authentication Code,它是一种基于分组密码的消息认证码算法是基于密码的MAC,只提供一个分组密码如AES,就可以构造MAC。
CBC-MAC是最早的CMAC,其用CBC模式对全0初始值IV下的消息M进行加密,并只保留最后一组密文作为消息M的标签.基本的计算过程就是分别计算C1=E(K,M1),C2=E(K,M2⊗C1),C3=E(K,M3⊗C2)...对M的每个分组只保留最后的Ci,这就是经过CBC-MAC的M的标签。
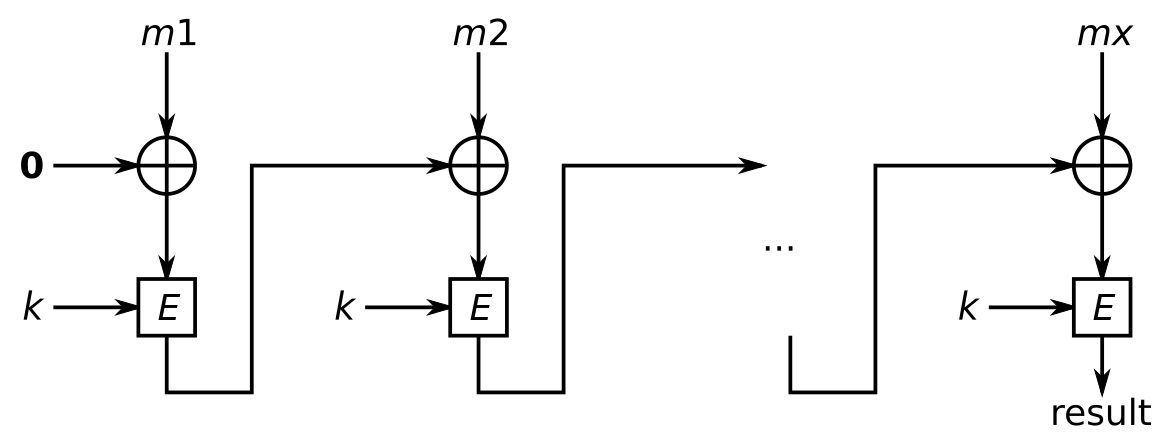
其容易被攻击者构造出新的消息-标签对。攻击流程如下
设存在两个不同的消息M1,M2,对应的标签分别为T1=E(K,M1),T2=E(K,M2),攻击者由此可以构造出新的消息-标签对,即消息M1||(M2⊗T1)的标签为T2,推导过程如下:
要对M1||(M2⊗T1)生成标签,则先要计算C1=E(K,M1)=T1,然后计算C2=E(K,(M2⊗T1)⊗T1))=E(K,M2)=T2
由此,攻击者就从两个消息-标签对,且不知道密钥的情况下构造出了新的消息-标签对,这意味着攻击者可以伪造CBC-MAC的标签,所以CBC-MAC并不安全
AE,Authenticated encryption,即认证加密,这既能实现消息的保密,又能保护消息的真实性,即实现认证。所以一个AE算法既有密码算法的特性又有MAC的特性。要实现AE,如下图所示有三种方式:
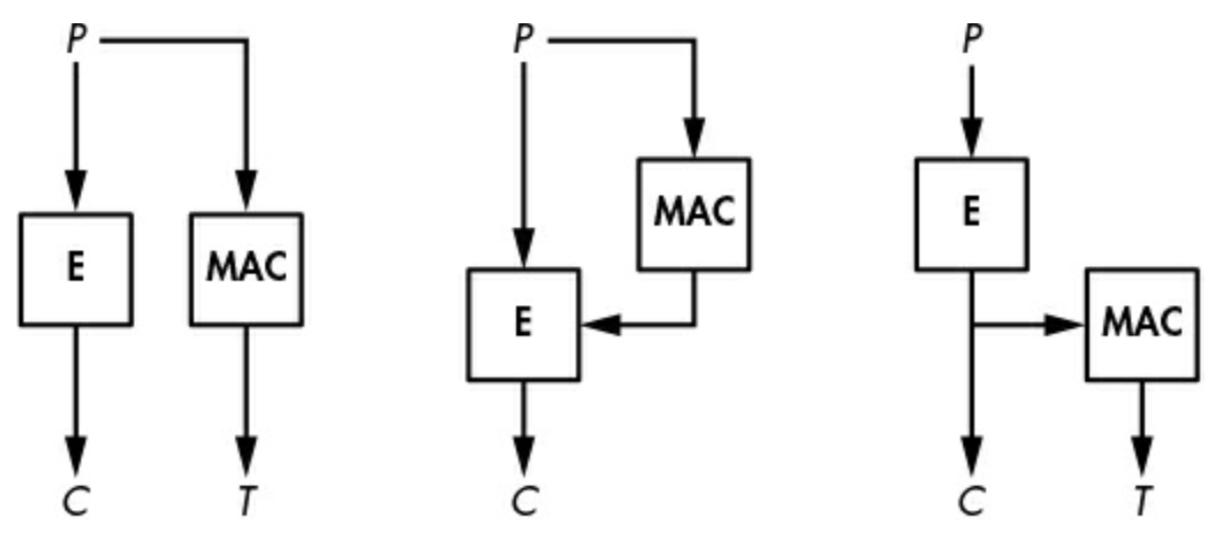
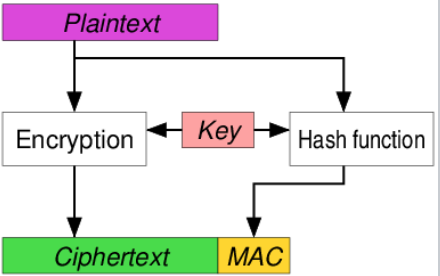
发送方:给定明文P,计算得到密文C=E(K1,P),同时计算得到认证标签T=MAC(K2,P),发送C,T
接收方:计算P=D(K1,C)得到P,然后用这个P计算MAC(K2,P),将结果与收到的T比较。如果C或T损坏,认证都会失败。
这个方案理论上是最不安全的。即使用的是安全的MAC,也有可能从中泄露明文P的信息,因为MAC仅用于确保不可伪造,不能确保随机。除非用的MAC非常强大,比如伪随机函数等。
SSH使用的就是这种方案,其用的MAC是HMAC-SHA-256,保证了不会泄露P的信息
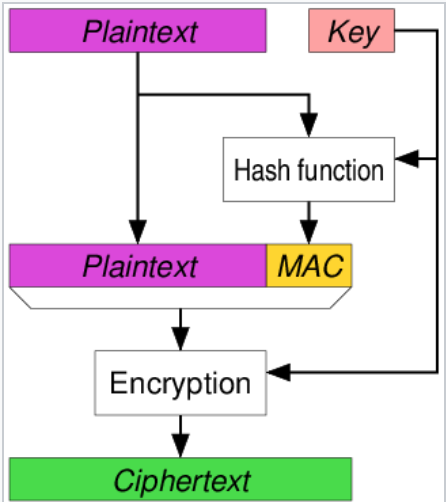
发送方:首先计算T=MAC(K2,P)来保护消息P,然后加密得到C=E(K1,P||T),这里将明文和标签一起加密,得到密文。发送方发送C
接收方:解密C,即P||T=D(K1,C)得到P||T,然后通过得到的明文P计算标签MAC(K2,P),并与得到的T比较,如果符合,则认证成功。
这种方式隐藏了明文的认证标签,从而防止标签泄露明文中的认证信息。
在TLS1.3之前,都是使用该方案。
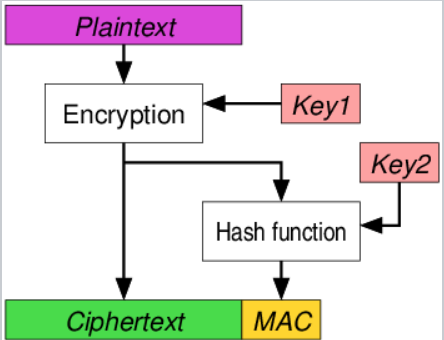
发送方:首先加密得到密文C=E(K1,P),然后计算认证标签T=MAC(K2,C),将其发送
接收方:使用MAC(K2,C)计算结果与收到的T比较,若相符,则再计算P=D(K1,C),得到明文。
这个方案的优势在于:1.接收方只需要计算MAC就可知道信息是否损坏,如果损坏就不需要进一步解密了;2.对于攻击者而言,除非能破解MAC,否则不能同时将C和T发送给接收方获得解密结果,这使得攻击者更难向接收方发送恶意数据
所以这种方案是三者之间最安全的,IPSec使用了方案
除了如上三种,组成起来实现,也有专门的认证加密算法,其可以表示为
加密:AE(K,P)=(C,T),K是密钥,P是明文,C是密文,T是身份认证标签
解密:AD(K,C,T)=P,如果C,T至少有一个无效,则AD会返回错误,而如果返回明文,则可以确保这个明文是被用正确密钥加密过的明文。
从认证角度看,其功能与MAC一样,这意味着想要伪造AD能接收并解密的密文和标记对(C,T)是不可能的
从加密角度看,认证加密比普通密码算法更安全,因为它只有在标签有效的情况下才会用密钥进行解密。这可以防止选择密文攻击。
认证加密算法中目前唯一被承认的正式标准就是AES-GCM,其基于AES算法,采用Galois计数器模式(GCM)实施。其示意图如下
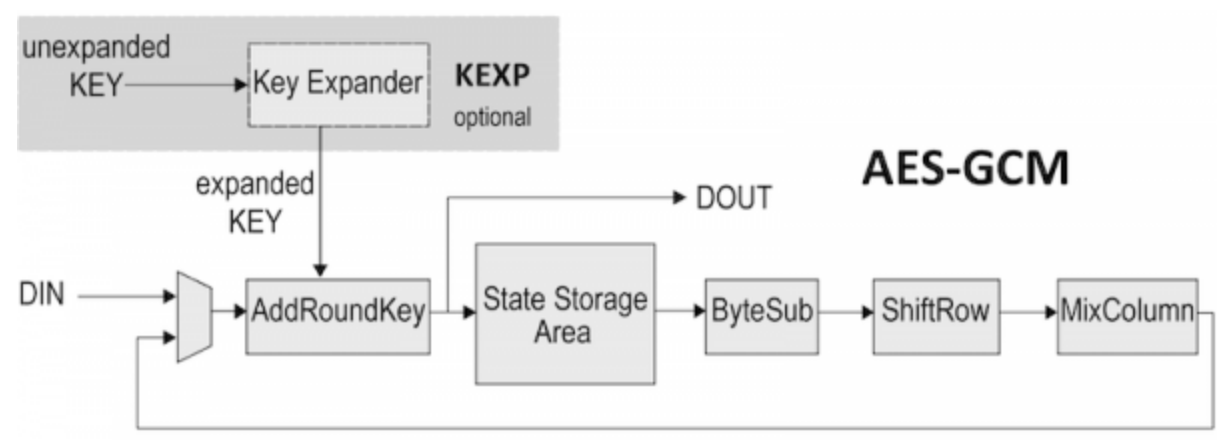
GCM本质上是对CTR模式的改进,集成了一个小组件计算身份认证标签,其示意如下
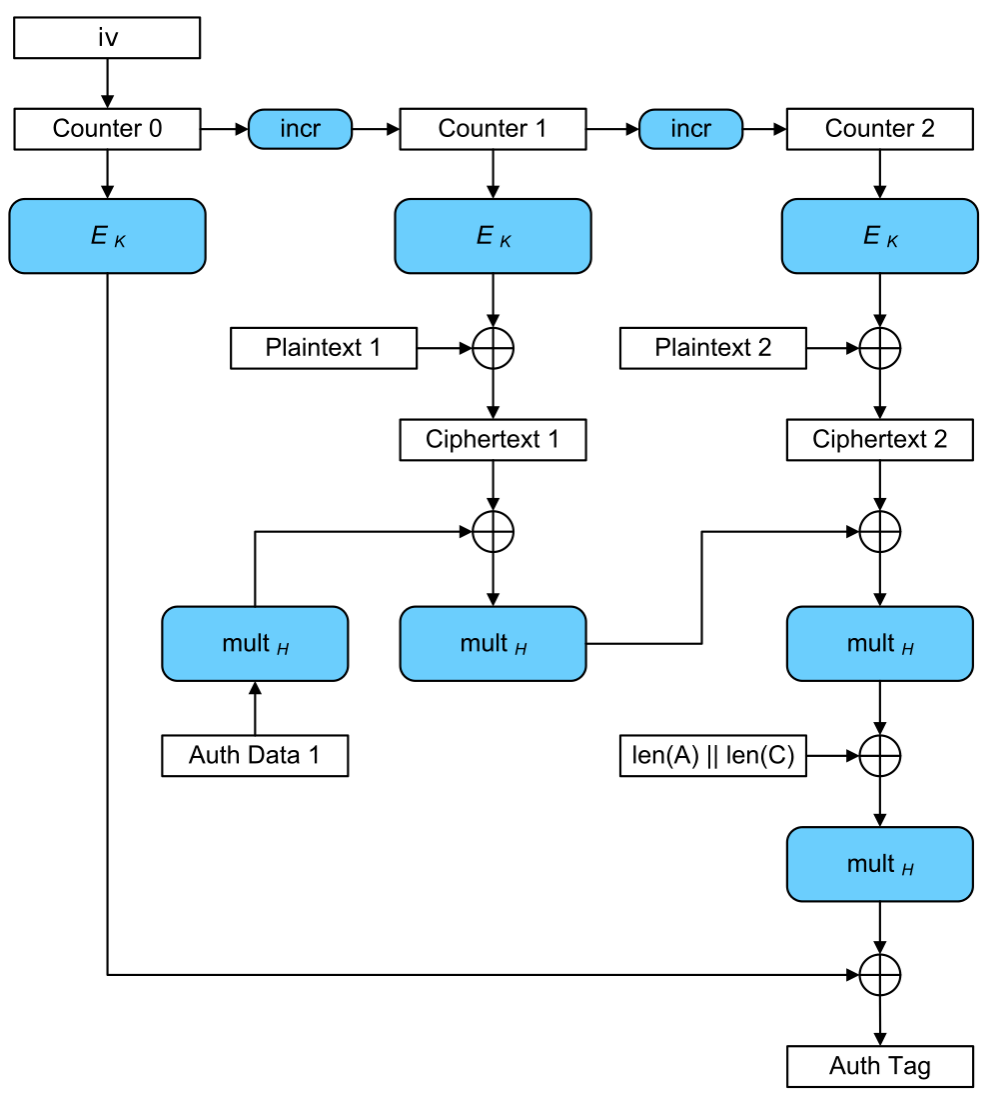
AES-GCM容易受到攻击,包括nonce重放攻击以及由弱哈希密钥、短标签等引发的攻击。
这是AES-GCM最大的漏洞。如果用户在两次AES-GCM中使用相同的nonce N,攻击者就可以获得身份认证密钥H,继而可以使用H为任何密文、关联数据伪造标签。
其基本代数结构如下
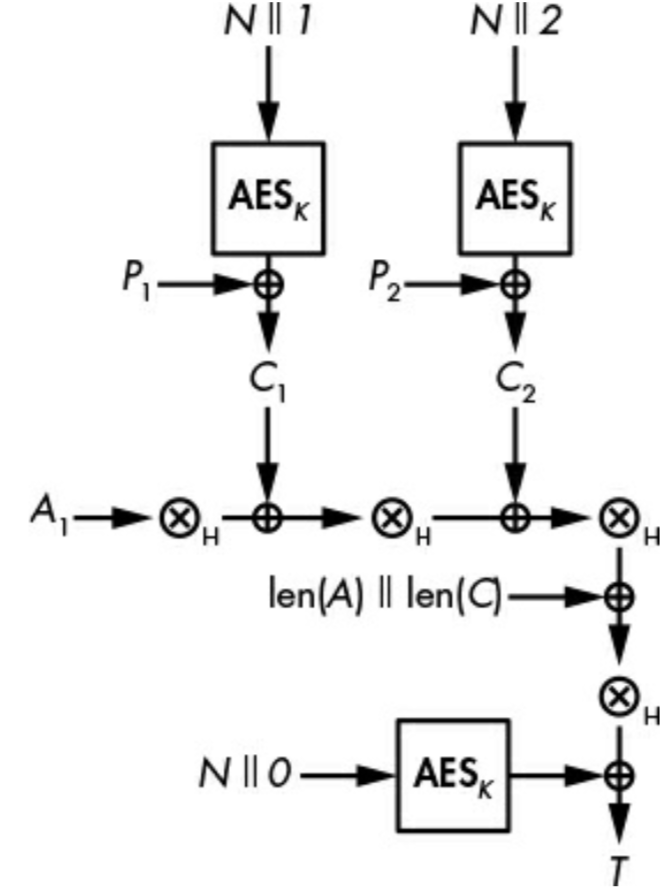
标签T通过下式计算得到:
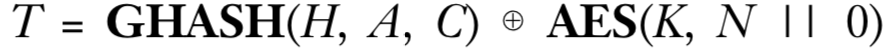
上式中的GHASH是一个通用哈希函数,其输入输出线性相关
此时如果有用相同nonce计算得到的两个标签T1,T2,将其异或可以得到
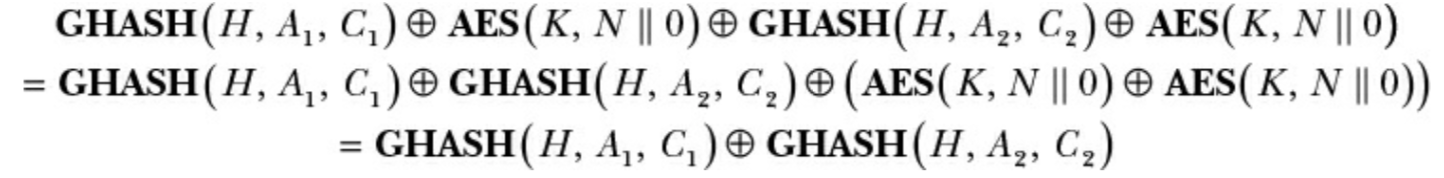
可以看到,此时AES的部分就消去了
然后利用GHASH的线性特性,攻击者就可以确定H,从而拿到身份认证密钥
GHASH存在重大缺陷,哈希密钥H的某些取值大大简化了对GCM认证机制的攻击,概括来说,如果H的取值属于某个特定的数学上定义的子群中时,攻击者可以通过仅仅对前一条消息分组进行变换从而猜测出某个消息的身份认证标签T。
GHASH的内部结构我们这里略去,直接到最后一步,此时有
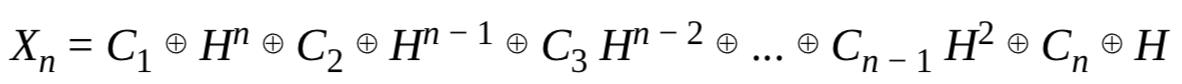
GHASH将消息的长度与Xn异或,将结果乘以H,然后将这个值与AES(K,N||0)异或,从而得到身份认证标签T
这里的漏洞在于,如果H=0,则不论Ci为何值都有Xn=0,与消息无关。这意味着,如果H=0,那么所有的消息都会具有相同的身份认证标签;而如果H=1,那么标签实际上只是密文分组的异或,这样会导致重新排序的密文分组会有相同的身份认证标签。
当然,除了H=0,H=1之外,当H取其他值时也会发生异常情况。例如基于5阶循环群的例子,设H=10d04d25f93556e69f58ce2f8d035a4,这是一个属于长度为5的循环的,H的取值满足H^5=H,那么对任何5的倍数e,都有
H^e=H
那么在前面的Xn的表达式中,交换分组Cn(和H相乘)和分组Cn-4(和H^5相乘)不会改变身份认证标签,这实际上就相当于伪造了。即,攻击者可在不知道密钥的情况下,利用这个属性构造新的消息及其有效认证标签。
更详细的分析可以阅读论文《Cycling Attacks on GCM, GHASH and Other Polynomial MACs and Hashes》
实际中AES-GCM通常返回128比特的标签,不过它可以生成任意长度的标签,但是长度越小,被伪造的可能性越高。
使用128比特长度时,伪造成功的概率为1/2^128;但是,由于GCM结构内在缺陷,当长度较短时,伪造的概率要大于
1/2^n
比如如果长度为32比特,则成功伪造的概率为1/2^16而不是我们以为的
1/2^32
根据Ferguson的论文指出,对于n比特标签,成功伪造概率为2^m/
2^n
其中2^m是攻击者能够获得的对应标签的最长消息的分组数目。
举个例子,如果使用48比特的标签去处理4GB的消息(2^28个块),
那么能够伪造的概率为2^20,这在密码学中是一个很高的概率了。
更详细的分析可以阅读论文《AuthenticationweaknessesinGCM》
RSA加密算法是一种非对称加密算法,在公开密钥加密和电子商业中被广泛使用。RSA是由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)在1977年一起提出的.RSA的工作原理就是创建一个被称为陷门置换的数学对象。陷门置换描述的是符合下述性质的函数:
将数字x变换为同一范围内的数字y,除非知道私钥,否则不能从y计算得到x,这个私钥就称为陷门.
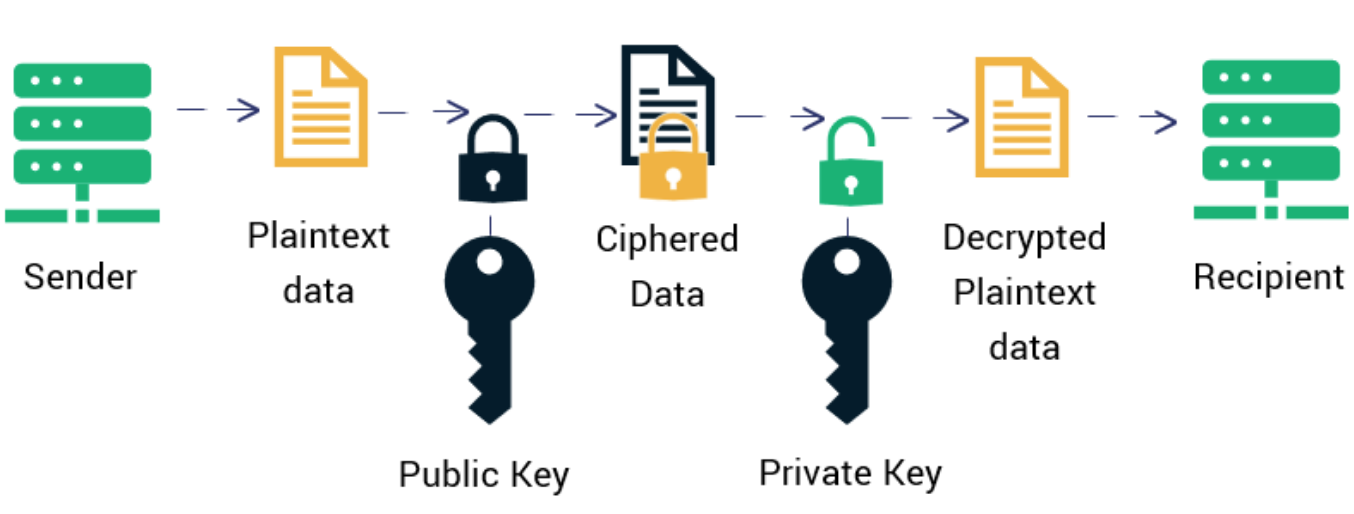
陷门置换是RSA的核心。给定模数n和公开指数e,RSA陷门置换将群Zn中的数x通过y= x^e mod n变换为群Zn中的另一个数y。
在加密时,n和e就是RSA的公钥
为了能够从y计算出x,则需要另一个数d,通过如下计算得到x

d就是陷门,也是RSA私钥的一部分,d也被称为秘密指数
d并不能任意取值,其必须满足
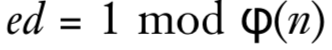
这样才能得到
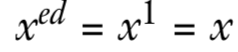
这里需要注意,我们用的是模φ(n)而不是模n
φ(n)=(p-1)(q-1),这个数对RSA的安全性至关重要,如果攻击者能从模数n中求出φ(n),就等价于破解了RSA。这是因为如果知道φ(n),在计算e模φ(n)的逆,就可以得到d。为此,p和q也应该保密,因为φ(n)可以由其计算得到
整个RSA的安全级别取决于n的大小、p与q的选择、陷门置换的应用;如果n太小,则容易对其分解,从而泄露私钥;如果p与q太小或者太接近,则容易从n中确定出相应取值;陷门置换不应该被直接用于签名或加密
在教科书中的RSA介绍中,通常会看到误用陷门置换的情况,其被直接用于加密或者签名了。即,RSA中的明文只是要加密的消息。这看起来没问题,实际上存在很大的风险。
这种教科书式的RSA加密是确定性的,即对同一明文加密两次,得到的密文是相同的。除此之外,更大的问题是,当给定两个密文y1=x1^e mod n和
y2=x2^e mod n时,攻击者可以通过将其相乘,得到明文x1xx2的密文:
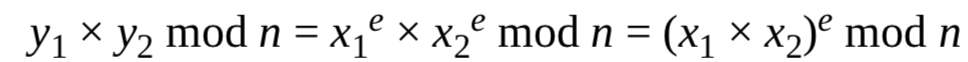
这个结果就是消息x1xx2 mod n对应的密文,这意味着,攻击者可以从两个RSA密文中构造出新的有效密文。这种弱点我们称之为扩展性风险(安全的密码应该确保只有在知道x1,x2时才能得到两者相乘的密文,如果只知道y1,y2是不能够得到的)
为了使RSA不可扩展,提出了OAEP,其中密文由待加密消息和一些padding组成,他们一起组成了RSA-OAEP。
OAEP的示意图如下
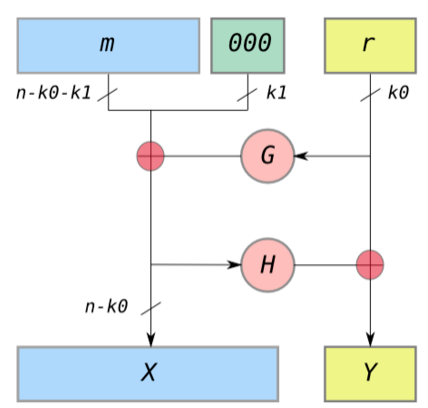
图中, n是RSA模数的位数,k0和k1是协议中的固定整数。m是n-k0-k1位长的明文消息,G和H是随机预言,如加密散列函数,⊕是异或运算。
编码过程包括如下步骤:
用 k1 位长的 0 将消息填充至 n - k0 位的长度。
随机生成 k0 位长的串 r
用 G 将k0 位长的 r 扩展至 n - k0 位长。
X = m00...0 ⊕ G(r)
H 将 n - k0 位长的 X 缩短至 k0 位长。
Y = r ⊕ H(X)
输出为 X || Y,在图中 X 为最左边的块,Y 位最右边的块。
随后可以使用 RSA 加密编码的消息
解码过程包括如下步骤:
恢复随机串 r 为 Y⊕H(X)
恢复消息 m00...0 为 X ⊕ G(r)
教科书中的RSA签名同样是简化过的,通过直接计算y = x^d mod n对消息x进行签名。这虽然简单,便于初学者理解,但是其存在签名被伪造的风险。
举个最简单的例子,因为有
0^d mod n=0
1^d mod n=1
(n-1)^d mod n = n-1
那么攻击者一直可以在不知道d的情况下伪造0,1,n-1的签名
更严重的攻击手段我们称之为盲签名攻击,即消息M不会被受害者主动签名,但是攻击者可以让M被受害者签名。攻击流程如下
1.攻击者找到某个值R,R^eM mod n是受害者会签名的一条信息,此时得到的签名记做S=(R^eM)^d mod n,现在的问题就是攻击者怎样能得到M的签名,即M^d
2.推导如下
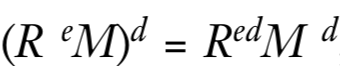
且
![]()
所以有
S=(ReM)^d
RM^d
为了得到M^d,将S除R即可
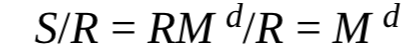
为了避免这种攻击,提出了RSA概率签名方案PSS,PSS之于RSA签名等同于OAEP之于RSA加密,它能让签名更安全,其流程比较复杂,基本示意图如下
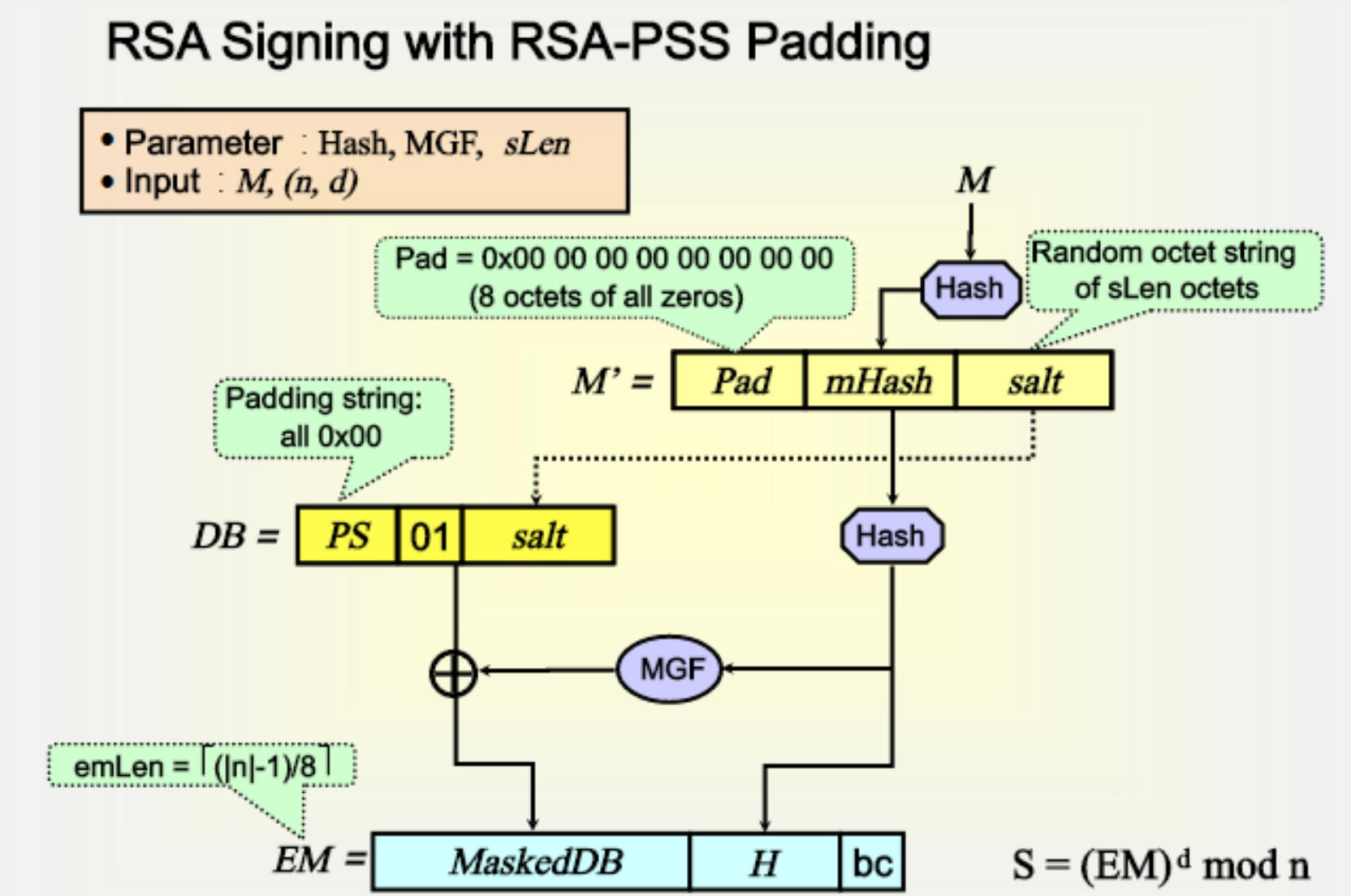
此外还有更简单的签名方案,即FDH,全域哈希。
Bellcore攻击属于错误攻击的一种,其迫使算法的一部分执行不当,产生错误的结果,将其与正确结果相比较,从而获得关于算法内部值的信息。
Bellcore适用于使用中国剩余定理的确定性的RSA签名方案。
由相关基础知识,我们有
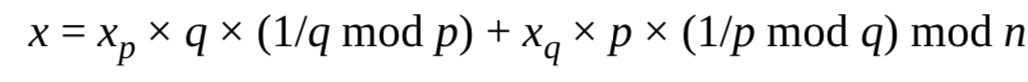
其中
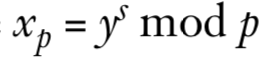
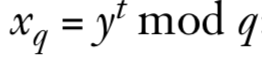
假设攻击者在就按xq时产生错误,得到错误值xq’,继续使用xq‘并得到相应的x’。那么攻击者现在就可以计算正确的签名x和错误的签名x‘的差,并由此分解模数n:
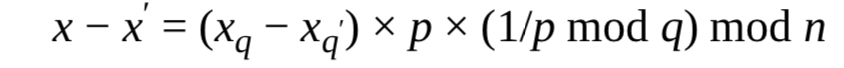
由上式,x-x'是p的倍数,即p是x-x'的除数,由于p也是n的除数,所以n和x-x'的最大公约数是p,即
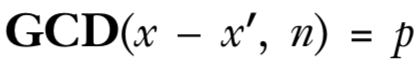
然后就可以计算出q=n/p以及d,从而破解RSA签名
我们直接举个例子。
设攻击者的私钥为(n,d1),受害者的私钥为(n,d2),受害者公钥为(n,e2),此时攻击者知道n,不知道p和q,所以不能从公开指数e2计算秘密指数d2。那么怎么从d中计算出p和q呢?
我们知道d和e满足
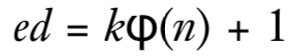
虽然我们不知道d或φ(n),但是我们可以计算出kφ(n)=ed-1
根据欧拉定理,对于任何一个与n互素的数a,有a^(φ(n))=1 mod n,所以,对模数n,有下式:
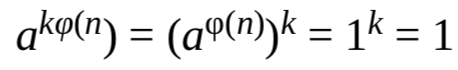
由于kφ(n)是偶数,所以可以写成2^st,所以可以把
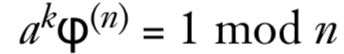
写成如下形式
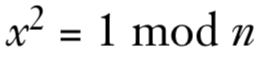
式子中的x可以通过kφ(n)计算得到
x^2-1=(x-1)(x+1),这意味
x^2-1可以被n整除,即x-1或x+1二者必有其一与n有相同的因数,从而可以算出n的因数,从而攻破RSA。
1.https://link.springer.com/content/pdf/10.1007%2F0-387-34805-0_39.pdf
2.《foundations of cryptography》
3.https://link.springer.com/chapter/10.1007/3-540-68697-5_1
4.https://eprint.iacr.org/2006/043.pdf
5.https://link.springer.com/chapter/10.1007/978-3-540-74143-5_2
6.https://www.cs.ucdavis.edu/~rogaway/papers/ae.pdf
7.https://link.springer.com/chapter/10.1007/978-3-642-34047-5_13
9.https://competitions.cr.yp.to/caesar.html
10.https://www.sciencedirect.com/science/article/abs/pii/S1574013715300290
本课程最终解释权归蚁景网安学院
本页面信息仅供参考,请扫码咨询客服了解本课程最新内容和活动